At the atomic level, montmorillonite is built up of so-called TOT-layers: covalently bonded sheets of aluminum (“O”) and silica (“T”) oxide (including the right amount of impurities/defects). In my mind, such TOT-layers make up the fundamental particles of a bentonite sample. Reasonably, since montmorillonite TOT-layers vary extensively in size, and since a single cubic centimeter of bentonite contains about ten million billions (\(10^{16}\)), they are generally configured in some crazily complicated manner.
Stack descriptions in the literature
But the idea that the single TOT-layer is the fundamental building block of bentonite is not shared with many of today’s bentonite researchers. Instead, you find descriptions like e.g. this one, from Bacle et al. (2016)
Clay mineral particles consist of stacks of parallel negatively-charged layers separated by interlayer nanopores. Consequently, compacted smectite contains two major classes of pores: interlayer nanopores (located inside the particles) and larger mesopores (located between the particles).
or this one, from Churakov et al. (2014)
In compacted rocks, montmorillonite (Mt) forms aggregates (particles) with 5–20 TOT layers (Segad et al., 2010). A typical radial size of these particles is of the order of 0.01 to 1 \(\mathrm{\mu m}\). The pore space between Mt particles is referred to as interparticle porosity. Depending on the degree of compaction, the interparticle porosity contributes 10 to 30% of the total water accessible pore space in Mt (Holmboe et al., 2012; Kozaki et al., 2001).
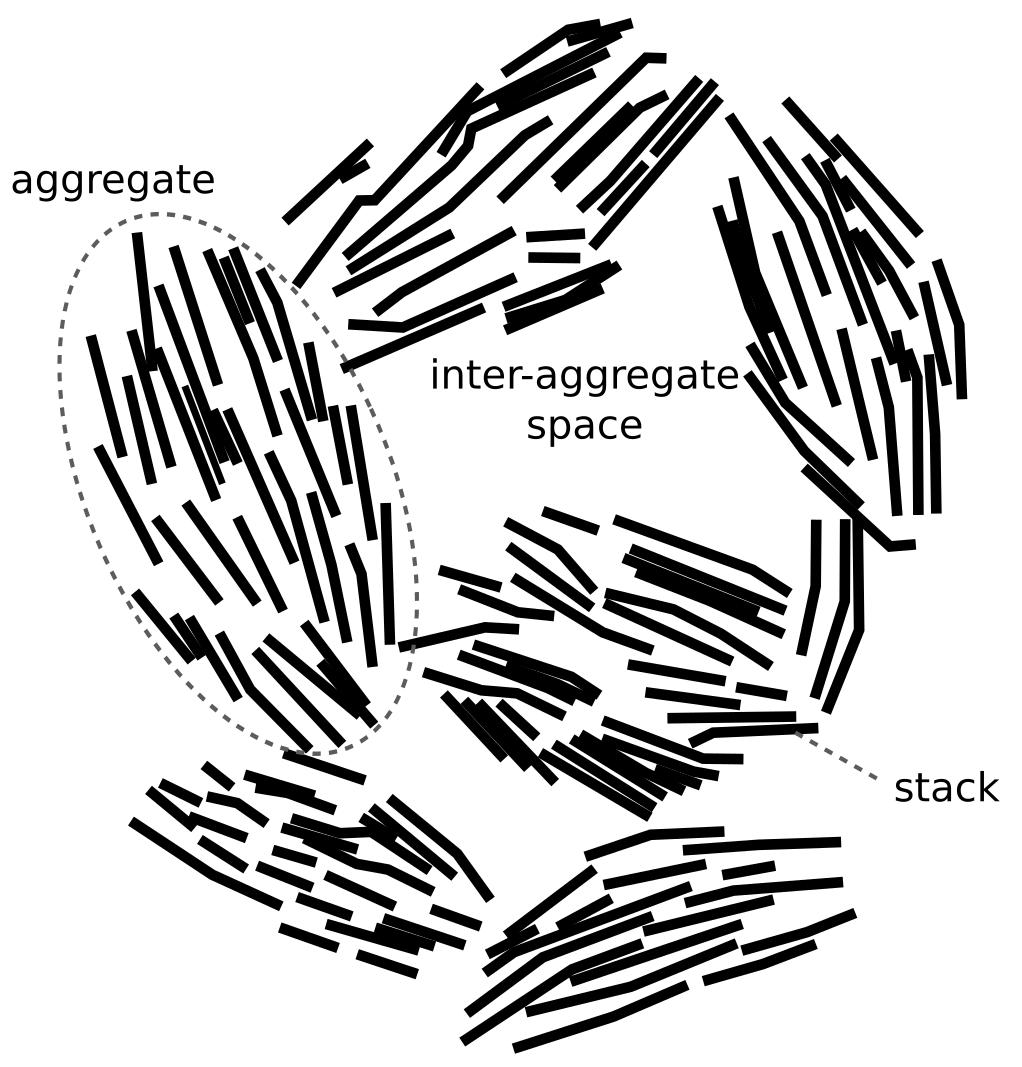
Here it is clear that they differ between “aggregates” (which I’m not sure is the same thing as “particles”), “stacks”, and individual TOT-layers (which I assume are represented by the line-shaped objects). In the following, however, we will use the term “stack” to refer to any kind of suggested fundamental structure built up from individual TOT-layers.
The one-sentence version of this blog post is:
Stacks make no sense as fundamental building blocks in models of water saturated, compacted bentonite.
The easiest argument against stacks is, in my mind, to simply work out the geometrical consequences. But before doing that we will examine some of the references given to support statements about stacks in compacted systems. Often, no references are given at all, but when they are, they usually turn out to be largely irrelevant for the system under study, or even to support an opposite view.
Inadequate referencing
As an example (of many) of inadequate referencing, we use the statement above from Churakov et al. (2014) as a starting point. I think this is a “good” statement, in the sense that it makes rather precise claims about how compacted bentonite is supposed to be structured, and provides references for some key statements, which makes it easier to criticize.
Churakov et al. (2014) reference Segad et al. (2010) for the statement that montmorillonite forms “particles” with 5 – 20 TOT-layers. In turn, Segad et al. (2010) write:
Clay is normally not a homogeneous lamellar material. It might be better described as a disordered structure of stacks of platelets, sometimes called tactoids — a tactoid typically consists of 5-20 platelets.19-21
Here the terminology is quite different from the previous quotations: TOT-layers are called “platelets”, and “particles” are called “tactoids”. Still, they use the phrase “stacks of platelets”, so I think we can continue with using “stack” as a sort of common term for what is being discussed.1 We may also note that here is used the word “clay”, rather than “montmorillonite” (as does Bacle et al. (2016)), but it is clear from the context of the article that it really is montmorillonite/bentonite that is discussed.
Anyhow, Segad et al. (2010) do not give much direct information on the claim we investigate, but provide three new references. Two2 of these — Banin (1967) and Shalkevich et al. (2007) — are actually studies on montmorillonite suspensions, i.e. as far away as you can get from compacted bentonite in terms of density; the solid mass fraction in these studies is in the range 1 – 4%.
The average distance between individual TOT-layers in this density limit is comparable with, or even larger than, their typical lateral extension (~100 nm). Therefore, much of the behavior of low density montmorillonite depends critically on details of the interaction between layer edges and various other components, and systems in this density limit behave very differently depending on e.g. ionic strength, cation population, preparation protocol, temperature, time, etc. This complex behavior is also connected with the fact that pure Ca-montmorillonite does not form a sol, while the presence of as little as 10 – 20% sodium makes the system sol forming. The behaviors and structures of montmorillonite suspensions, however, say very little about how the TOT-layers are organized in compacted bentonite.
We have thus propagated from a statement in Churakov et al. (2014), and a similar one in Segad et al. (2010), that montmorillonite in general, in “compacted rocks” forms aggregates of 5 – 20 TOT-layers, to studies which essentially concern different types of materials. Moreover, the actual value of “5 – 20 TOT layers” comes from Banin (1967), who writes
Evidence has accumulated showing that when montmorillonite is adsorbed with Ca, stable tactoids, containing 5 to 20 parallel plates, are formed (1). When the mineral is adsorbed with Na, the tactoids are not stable, and the single plates are separated from each other.
This source consequently claims that the single TOT-layers are the fundamental units, i.e. it provides an argument against any stack concept! (It basically states that pure Ca-montmorillonite does not form a sol.) In the same manner, even though Segad et al. (2010) make the above quoted statement in the beginning of the paper, they only conclude that “tactoids” are formed in pure Ca-montmorillonite.
The swelling and sedimentation behavior of Ca-montmorillonite is a very interesting question, that we do not have all the answers to yet. Still, it is basically irrelevant for making statements about the structure in compacted — sodium dominated3 — bentonite.
Churakov et al. (2014) also give two references for the statement that the “interparticle porosity” in montmorillonite is 10 – 30% of the total porosity: Holmboe et al. (2012) and Kozaki et al. (2001). This is a bizarre way of referencing, as these two studies draw incompatible conclusions, and since Holmboe et al. (2012) — which is the more adequately performed study — state that this type of porosity may be absent:
At dry density \(>1.4 \;\mathrm{g/cm^3}\) , the average interparticle porosity for the [natural Na-dominated bentonite and purified Na-montmorillonite] samples used in this study was found to be \(1.5\pm1.5\%\), i.e. \(\le 3\%\) and significantly lower than previously reported in the literature.
Holmboe et al. (2012) address directly the discrepancy with earlier studies, and suggest that these were not properly analyzed
The apparent discrepancy between the basal spacings reported by Kozaki et al. (1998, 2001) using Kunipia-F washed Na-montmorillonite, and by Muurinen et al. (2004), using a Na-montmorillonite originating from Wyoming Bentonite MX-80, and the corresponding average basal spacings of the [Na-montmorillonite originating from Wyoming bentonite MX-80] samples reported in this study may partly be due to water contents and partly to the fact that only apparent \(\mathrm{d_{001}}\) values using Bragg’s law, without any profile fitting, were reported in their studies.
If Kozaki et al. (2001) should be used to support a claim about “interparticle porosity”, it consequently has to be done in opposition to — not in conjunction with — Holmboe et al. (2012). It would then also be appropriate for authors to provide arguments for why they discard the conclusions of Holmboe et al. (2012).4
Stacks in compacted bentonite make no geometrical sense
The literature is full of fancy figures of bentonite structure involving stacks. A typical example is found in Wu et al. (2018), and looks similar to this:
This illustration is part of a figure with the caption “Schematic representation of the different porosities in bentonite and the potential diffusion paths.”5 The regular rectangles in this picture illustrate stacks that each seems to contain five TOT-layers (I assume this throughout). Conveniently, these groups of five layers have the same length within each stack, while the length varies somewhat between stacks. This is a quite common feature in figures like this, but it is also common that all stacks are given the same length.
Another feature this illustration has in common with others is that the particles are ordered: we are always shown edges of the TOT-layers. I guess this is partly because a picture of a bunch of stacks seen from “the top” would be less interesting, but it also emphasizes the problem of representing the third dimension: figures like these are in practice figures of straight lines oriented in 2D, and the viewer is implicitly required to imagine a 3D-version of this two-dimensional representation.
A “realistic” stack picture
But, even as a 2D-representation, these figures are not representative of what an actual configuration of stacks of TOT-layers looks like. Individual TOT-layers have a distinct thickness of about 1 nm, but varies widely in the other two dimensions. Ploehn and Liu (2006) analyzed the size distribution of Na-montmorillonite (“Cloisite Na+”) using atomic force microscopy, and found an average aspect ratio of 180 (square-root of basal area divided by thickness). A representative single “TOT-line” drawn to scale is consequently quite different from what is illustrated in in most stack-pictures, and look like this (click on the figure to see it in full size)
In this figure, we have added “water layers” on each side of the TOT-layer (light red), with the water-to-solid volume ratio of 16. Neatly stacking five such units shows that the rectangles in the Wu et al. (2018)-figure should be transformed like this
But this is still not representative of what an assemblage of five randomly picked TOT-layers would look like, because the size distribution has a substantial variance. According to Ploehn and Liu (2006), the aspect ratio follows approximately a log-normal distribution. If we draw five values from this distribution for the length of five “TOT-lines”, and form assemblages, we end up with structures that look like this:7
These are the kind of units that should fill the bentonite illustrations. They are quite irregularly shaped and are certainly not identical (this would be even more pronounced when considering the third dimension, and if the stacks contain more layers).
It is easy to see that it is impossible to construct a dense structure with these building blocks, if they are allowed a random orientation. The resulting structure rather looks something like this
Such a structure evidently has very low density, and are reminiscent of the gel structures suggested in e.g. Shalkevich et al. (2007) (see fig. 7 in that paper). This makes some sense, since the idea of stacks of TOT-layers (“tactoids”) originated from studies of low density structures, as discussed above.
Note that the structure in pictures like that in Wu et al. (2018) has a substantial density only because it is constructed with stacks with an unrealistic shape. But even in these types of pictures is the density not very high: with some rudimentary image analysis we conclude that the density in the above picture is only around 800 kg/m3. Also the figure from Navarro et al. (2017) above gives a density below 1000 kg/m3, although there it is explicitly stated that it is a representation of “highly compacted bentonite”.
The only manner in which the “realistic” building blocks can be made to form a dense structure is to keep them in the same orientation. The resulting structures then look e.g. like this
where we have color coded each stack, to remind ourselves that these units are supposed to be fundamental.
Just looking at this structure of a “stack of stacks” should make it clear how flawed the idea is of stacks as fundamental structural units in compacted bentonite (note also how unrepresentative the stack-pictures found in the literature are). One of many questions that immediately arises is e.g. why on earth the tiny gaps between stacks (indicated by arrows) should remain. This brings us to the next argument against stacks as fundamental units for compacted water saturated bentonite:
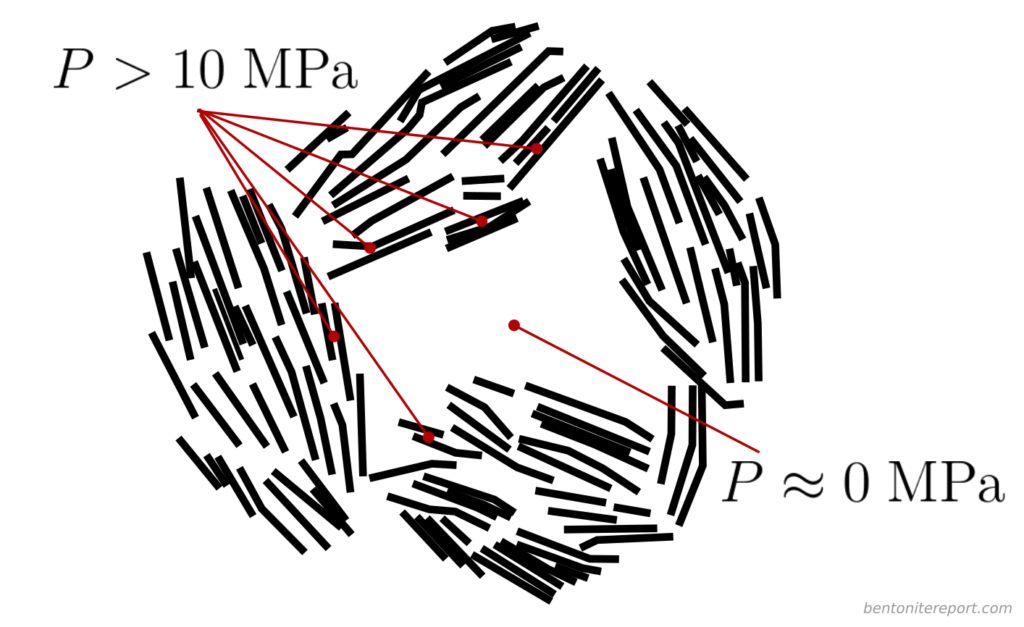
What is supposed to keep stacks together?
Assuming that this system is in equilibrium with an external water reservoir at zero pressure (i.e. atmospheric absolute pressure), the pressure in the compartment labeled “intra-aggregate space” is also close to zero. On the other hand, in the “stacks” located just a few nm away, the pressure is certainly above 10 MPa in many places! A structure like this is obviously not in mechanical equilibrium! (To use the term “obvious” here feels like such an understatement.)
Implications
To sum up what we have discussed so far, the following picture emerges. The bentonite literature is packed with descriptions of compacted water saturated bentonite as built up of stacks as fundamental units. These descriptions are so commonplace that they often are not supported by references. But when they are, it seems that the entire notion is based on misconceptions. In particular, structures identified in low density systems (suspensions, gels) have been carried over, without reflection, to descriptions of compacted bentonite. Moreover, all figures illustrating the stack concept are based on inadequate representations of what an arbitrary assemblage of TOT-layers arranged in this way actually would look like. With a “realistic” representation it quickly becomes obvious that it makes little sense to base a fundamental unit in compacted systems on the stack concept.
My impression is that this flawed stack concept underlies the entire contemporary mainstream view of compacted bentonite, as e.g. expressed by Wu et al. (2018):
A widely accepted view is that the total porosity of bentonite consists of \(\epsilon_ {ip}\) and \(\epsilon_ {il}\) (Tachi and Yotsuji, 2014; Tournassat and Appelo, 2011; Van Loon et al., 2007). \(\epsilon_ {ip}\) is a porosity related to the space between the bentonite particles and/or between the other grains of minerals present in bentonite. It can further be subdivided into \(\epsilon_ {ddl}\) and \(\epsilon_ {free}\). The diffuse double layer, which forms in the transition zone from the mineral surface to the free water space, contains water, cations and a minor amount of anions. The charge at the negative outer surface of the montmorillonite is neutralized by an excess of cations. The free water space contains a charge-balanced aqueous solution of cations and anions. \(\epsilon_ {il}\) represents the space between TOT-layers in montmorillonite particles exhibiting negatively charged surfaces. Due to anion exclusion effect, anions are excluded from the interlayer space, but water and cations are present.
This view can be summarized as:
- The fundamental building blocks are stacks of TOT-layers (“particles”, “aggregates”, “tactoids”, “grains”…)
- Electric double layers are present only on external surfaces of the stacks.
- Far away from external surfaces — in the “inter-particle” or “inter-aggregate” pores — the diffuse layers merge with a bulk water solution
- Interlayer pores are defined as being internal to the stacks, and are postulated to be fundamentally different from the external diffuse layers; they play by a different set of rules.
I don’t understand how authors can get away with promoting this conceptual view without supplying reasonable arguments for all of its assumptions8 — and with such a complex structure, there are a lot of assumptions.
As already discussed, the geometrical implications of the suggested structure do not hold up to scrutiny. Likewise, there are many arguments against the presence of substantial amounts of bulk water in compacted bentonite, including the pressure consideration above. But let’s also take a look at what is stated about “interlayers” and how these are distinguished from electric double layers (I will use quotation marks in the following, and write “interlayers” when specifically referring to pores defined as internal to stacks).
“Interlayers”
“Interlayers” are often postulated to be completely devoid of anions. We discussed this assumption in more depth in a previous blog post, where we discovered that the only references supplied when making this postulate are based on the Poisson-Boltzmann equation. But this is inadequate, since the Poisson-Boltzmann equation does describe diffuse layers, and predicts anions everywhere.
By requiring anion-free “interlayers”, authors actually claim that the physico-chemistry of “interlayers” is somehow qualitatively different from that of “external surfaces”, although these compartments have the exact same constitution (charged TOT-layer surface + ions + water). But an explanation for why this should be the case is never provided, nor is any argument given for why diffuse layer concepts are not supposed to apply to “interlayers”.9 This issue becomes even more absurd given the strong empirical evidence for that anions actually do reside in interlayers.
The treatment of anions is not the only ad hoc description of “interlayers”. It also seems close to mandatory to describe them as having a maximum extension, and as having an extension independently parameterized by sample density. E.g. the influential models for Na-bentonite of Bourg et al. (2006) and Tournassat and Appelo (2011) both rely on the idea that “interlayers” swell out to a certain volume that is smaller than the total pore volume, but that still depends on density.
In e.g. Bourg et al. (2006), the fraction of “interlayer” pores remains essentially constant at ~78%, as density decreases from 1.57 g/cm3 to 1.27 g/cm3, while the “interlayers” transform from having 2 monolayers of water (2WL) to having 3 monolayers (3WL). This is a very strange behavior: “interlayers” are acknowledged as having a swelling potential (2WL expands to 3WL), but do, for some reason, not affect 22% of the pore volume! Although such a behavior strongly deviates from what we expect if “interlayers” are treated with conventional diffuse layer concepts, no mechanism is provided.
In contrast, it should be noted that the established explanation for “tactoid” formation in pure Ca-montmorillonite involves no ad hoc assumptions of this sort, but rests on treating all ions as part of diffuse layers.
Another type of macabre consequence of defining “interlayer” pores as internal to stacks is that a completely homogeneous system is described has having no interlayer pores (because it has no stacks). E.g. Tournassat and Appelo (2011) write (\(n_c\) is the number of TOT-layers in a stack)
[…] the number of stacks in the \(c\)-direction has considerable influence on the interlayer porosity, with interlayer porosity increasing with \(n_c\) and reaching the maximum when \(n_c \approx 25\). The interlayer porosity halves with \(n_c\) when \(n_c\) is smaller than 3, and becomes zero for \(n_c = 1\).10
It is not acceptable that using the term interlayer should require accepting stacks as fundamental units. But the usage of the term as being internal to stacks is so widespread in the contemporary bentonite literature, that I fear it is difficult to even communicate this issue. Nevertheless, I am certain that e.g. Norrish (1954) does not depend on the existence of stacks when using the term like this:
Fig. 7 shows the relationship between interlayer spacing and water content for Na-montmorillonite. There is good agreement between the experimental points and the theoretical line, showing that interlayer swelling accounts for all, or almost all, of physical swelling.
The stack view obstructs real discovery
A severe consequence of the conceptual view just discussed is that “stacking number” — the (average) number of TOT-layers that stacks are supposed to contain — has been established as fitting parameter in models that are clearly over-parameterized. An example of this is Tournassat and Appelo (2011), who write11
Our predictive model excludes anions from the interlayer space and relates the interlayer porosity to the ionic strength and the montmorillonite bulk dry density. This presentation offers a good fit for measured anion accessible porosities in bentonites over a wide range of conditions and is also in agreement with microscopic observations.
But since anions do reside in interlayers,12 it would be better if the model didn’t fit: an over-parameterized or conceptually flawed model that fits data provides very little useful information.
A similar more recent example is Wu et al. (2018). In this work, a model based on the stack concept is successfully fitted both to data on \(\mathrm{ReO_4^-}\) diffusion in “GMZ” bentonite and to data on \(\mathrm{Cl^-}\) diffusion in “KWK” bentonite, by varying “stacking number” (among other parameters). Again, as the model assumes anion-free “interlayer” pores, a better outcome would be if it was not able to fit the data. Moreover, this paper focuses mainly on the ability of the model, while not at all emphasizing the fact that about ten (!) times more \(\mathrm{ReO_4^-}\) was measured in “GMZ” as compared with \(\mathrm{Cl^-}\) in “KWK”, at similar conditions in certain cases. The latter observation is quite puzzling and is, in my opinion, certainly worth deeper investigation (and I am fully convinced that it is not explained by differences in “stacking number”).
Footnotes
[1] The terminology in the bentonite literature is really all over the place. You may e.g. also find the term “tactoid” used as Navarro et al. (2017) use “aggregate”, or the term “platelet” used for a stack of TOT-layers…
[2] The third reference is an entire book on clays.
[3] Note that “sodium dominated” in this context means ~20% or more.
[4] It may be noticed that Kozaki et al. (2001) see no X-ray diffraction peaks for low density samples:
The basal spacing of water-saturated montmorillonite was determined by the XRD method. […] It was found that a basal spacing of 1.88 nm, corresponding to the three-water layer hydrate state […] was not observed before the dry density reached 1.0 Mg/m3.
My interpretation of this observation is that the diffraction peak has shifted to even lower reflection angles (in agreement with the observations of Holmboe et al. (2012)), not registered by the equipment. The alternative interpretation must otherwise be that “stacks” suddenly cease to exist below 1.0 g/cm3. (Yet, Kozaki et al. (2001) continues to use a certain d-value in their analysis, also for densities below 1.0 g/cm3.)
[5] I have discussed “diffusion paths” in an earlier blog post. This illustration certainly fits that discussion.
[6] A water-to-solid volume ratio of 1 corresponds basically to interlayers of three monolayers of water (3WL).
[7] To construct these units, I made the additional choice of placing each layer randomly in the horizontal direction, with the constraint that all layers should be confined within the range of the longest one in each unit.
[8] By “get away with” I mean “pass peer-review”, and by “don’t understand” I mean “understand”.
[9] This is reminiscent of how certain authors imply that the interlayer is non-diffusive under so-called crystalline swelling.
[10] A mathematical remark: if the interlayer porosity “halves with \(n_c\)” (what does that mean?) when \(n_c = 2\) (“smaller than 3”), it is impossible to simultaneously have zero interlayer porosity for \(n_c = 1\) (unless the interlayer porosity is zero for any \(n_c\)).
[11] I guess the word “presentation” here really should be “representation”?
[12] Note that one of the authors of this paper also claims in a later paper that anions do populate 3-waterlayer interlayers, in accordance with the Poisson-Boltzmann equation:
The agreement between PB calculations and MD simulation predictions was somewhat worse in the case of the \(\mathrm{Cl^-}\) concentration profiles than in the case of the \(\mathrm{Na^+}\) profiles (Figure 3), perhaps reflecting the poorer statistics for interlayer Cl concentrations […] Nevertheless, reasonable quantitative agreement was found (Table 2).